Aktualności
Różne formaty zapisów struktury
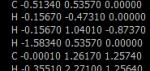
W modelowaniu molekularnym spotykamy różne formaty zapisu struktury związków, najpopularniejszymi formatami są układ kartezjański x,y,z, z-macierz, .pdb, czy .cif. Prawda jest taka, że istnieje cały szereg formatów zapisu, medot konwersji, rodzaju przydatności czy oprogramowania.
Wstęp do modelowania
Modelowanie Komputerowe
Modelowanie molekularne, zwane inaczej chemią obliczeniową, ma zastosowanie zarówno w chemii, biochemii, inżynierii materiałowej jak i w nanotechnologii. Rozwój komputerów oraz programów sprawił, że w ostatnich czasach stało się ono dostępne dla wszystkich, a obliczenia chemiczne można już przeprowadzać na komputerze osobistym. Koszt oraz czas badań teoretycznych jest niejednokrotnie o wiele mniejszy niż wstępne badania praktyczne a uzyskane wyniki coraz bardziej zbliżają się do wyników eksperymentalnych. Korzystając z dobrodziejstw chemii teoretycznej możemy już dziś z bardzo dobrymi rezultatami przewidzieć właściwości fizyczne i chemiczne, modelować reakcje oraz stany przejściowe, symulować widma spektroskopowe, czy też badać układy bardziej skomplikowane, jakim są centra aktywne enzymów. Możemy także projektować leki oraz nowe materiały. Modelowanie komputerowe często nie może dać jednoznacznej odpowiedzi na zadawane pytania, ale w znaczny sposób pomaga zrozumieć oraz rozwiązać problemy. Wszechstronnie wykształcony chemik powinien umieć korzystać z najnowszych dobrodziejstw, jakim niewątpliwie jest wsparcie badań eksperymentalnych obliczeniami.
Elektryczny moment dipolowy
 Elektryczny moment dipolowy jest wektorową wielkością fizyczną, która opisuje dipol. Dipol jest układem ładunków elektrycznych o tej samej wartości lecz posiadających przeciwny znak ... więcej w artykule Pawła Grabowskiego.
Elektryczny moment dipolowy jest wektorową wielkością fizyczną, która opisuje dipol. Dipol jest układem ładunków elektrycznych o tej samej wartości lecz posiadających przeciwny znak ... więcej w artykule Pawła Grabowskiego.
Potencjał korelacyjno-wymienny B3LYP

Hyperchem - jeszcze raz od podstaw
Mamy zaszczyt przedstawić fragment kursu autorstwa dr Piotra Wojciechowskiego z Politechniki Wrocławskiej. Fragment kursu opisuje pierwsze kroki w programie chemicznych HyperchemR. Oryginalna strona kursu znajduje się http://eportal-ch.pwr.wroc.pl Jeszcze raz dziękujemy autorowi za udostępnienie materiałów.
Struktura związków w przestrzeni X,Y,Z
Ćwiczenie
Struktura związków w przestrzeni X,Y,Z
Jednym ze sposobów zapisu struktury jest podanie współrzędnych kolejnych atomów w postaci położenia x,y,z – korzystając z poniższych danych przeprowadź wizualizacje podanych cząsteczek. Powinieneś otrzymać podobne wyniki jak przedstawiamy w galerii.
Amarant (E123) – barwnik organiczny używany jako barwnik spożywczy. Ma barwę ciemnoczerwoną oraz dobrą wytrzymałość na wysoką temperaturę i światło. Obecnie stosowany do barwienia nielicznych produktów spoŜywczych, takich jak: niskoprocentowe napoje alkoholowe oraz kawior, a także to barwienia produktów takich jak szminki.
Testowanie różnych metod i baz do obliczeń geometrii
Ćwiczenie
Testowanie różnych metod i baz do obliczeń geometrii
Obliczona geometria cząsteczki zależy od wybranej metody i bazy. Używając lepszych metod oraz baz, mamy większe prawdopodobieństwo, że obliczone parametry geometryczne zbliżą się do wartości eksperymentalnych, które wyznaczone są zawsze z pewnym błędem. Większa baza i dokładniejsza metoda pociągają za sobą większe wymagania sprzętowe. Dlatego zawsze wybierając metodę i bazę na podstawie studiów literaturowych z określonej dziedziny, w której chcemy prowadzić obliczenia, musimy oszacować, na jak dokładną metodę możemy sobie pozwolić.
Aby samemu zbadać, jaką różnice w parametrach geometrycznych (długość wiązań, kąty) dają różne metody przeprowadź optymalizację cząsteczki aldehydu mrówkowego H2C=O, oraz porównaj z wartościami eksperymentalnymi.[1] Obliczenia przeprowadź:
I za pomocą mechaniki kwantowej metodą Amber
II jedną z wybranych metod półempirycznych:
a) AM1,
b) PM3,
c) PM3MM,
d) CNDO,
e) INDO,
III metodami ab inito: HF, MP2 oraz metodami DFT: B3LYP, B3PW91 w trzech wybranych bazach:
a) STO-3G,
b) 3-21G,
c) 6-31G(d) równoważne w zapisie starej notacji 6-31G*,
d) 6-31G(d,p) równoważne w zapisie starej notacji 6-31G**,
e) 6-31+G(d,p) równoważne w zapisie starej notacji 6-31+G**,
f)* aug-pvdz,
Otrzymane wyniki porównaj z wartościami eksperymentalnymi wiedząc, że cząsteczka jest płaska oraz kąt tworzony przez atomy HCH wynosi 116.5°, długość wiązania C-H 1.116 Å, C=O 1.208 Å.
* Dodatkowo dla struktur z optymalizowanych metodami AM1 oraz B3LYP/6-31G(d) przeprowadź optymalizację metodą B3LYP/6-31G(d,p), porównaj czasy obliczeń. Od czego zależy czas przeprowadzonej optymalizacji?
[1] Dallos, M.; Müller, T.; Lischka, H.; Shepard, R., Geometry optimization of excited valence states of formaldehyde using analytical multireference configuration interaction singles and doubles and multireference averaged quadratic coupled-cluster gradients, and the conical intersection formed by the 1 1B1(σ-π*) and 2 1A1(π-π*) states. J. Chem. Phys. 2001, 114, (2), 746-757.
Analiza konformacyjna 1,3-difluoropropanu
Ćwiczenie
Analiza konformacyjna 1,3-difluoropropanu
Zmień wartości poszczególnych kątów dwuściennych cząsteczki 1,3-difluoropropanu. Następnie przeprowadź optymalizację. Znajdź wszystkie struktury w minimach
energetycznych poprzez startowanie z różnych konformerów.

Określ minimum globalne. Obliczenia przeprowadź metodą B3LYP w bazie 6-31G(d) oraz w metodzie PM3. Bazując na lepszej metodzie B3LYP, porównaj z wynikami uzyskanymi metodą PM3.
Badanie struktury przestrzennej hemoglobiny1 - posługiwanie się bazą PDB
 Ćwiczenie
Ćwiczenie
Badanie struktury przestrzennej hemoglobiny1 - posługiwanie się bazą PDB
Podczas modelowania układów biologicznych opartych na białkach pierwszym etapem jest uzyskanie struktury przestrzennej białka. Geometrię białka uzyskuje się z badań eksperymentalnych głównie z rentgenografii strukturalnej lub z badań techniką nuklearnego rezonansu magnetycznego (NMR). Białka o ustalonej już geometrii są zdeponowane w różnych bazach. Jedną z takich baz oferująca ok. 30 tysięcy struktur jest PDB (Protein Data Bank) dostępna pod adresem: http://www.rcsb.org/pdb/.
Po wejściu na stronę www.rscb.org/pdb/, wyszukiwanie odpowiedniej struktury zaczynamy od wpisania słów kluczowych. Wyszukiwanie hemoglobiny dokonujemy wpisując w polu Serach the Archive angielską nazwę: hemoglobin. Z uzyskanych rezultatów wybieramy odpowiednie białko np.:

Klikając na odpowiedni link (EXPLORE, lub numer 1BZ0), uzyskujemy więcej informacji o białku. Spakowaną strukturę białka pobieramy klikając ikonę . Po pobraniu struktury i jej rozpakowaniu, otwieramy ją odpowiednim programem. Struktura białka została ustalona metodami rentgenograficznymi związku z czym nie zawiera atomów wodoru, dlatego potrzebne jest uzupełnienie atomami wodoru brakujących miejsc.
G
Posługując się programem GaussView wybieramy z menu File opcję Open?, a następnie ustawiamy w opcji Pliki Typu: Brookhaven PDB Files (*.pdb *.ent) i otwieramy rozpakowany plik ze strukturą białka. Program, podczas ładowania struktury, proponuje dodanie atomów wodoru (Would you like to add hydrogens to your PDB structure?), zgadzamy się wybierając Yes. Po tych operacjach możemy przystąpić do analizowania struktury i odpowiedzi na pytania.
HyperChem
Posługując się programem HyperChem, wybieramy z menu File opcję Open, a następnie ustawiając w opcji Pliki typu: Brookhaven PDB (*.ENT), otwieramy rozpakowany plik ze strukturą białka. Uzupełnienie wodorami dokonujemy wybierając z menu Build opcję Add Hydrogens. Po tych operacjach możemy przystąpić do analizowania struktury i odpowiedzi na pytania.
Rasmol
Dodatkowe informacje oraz podejrzenie struktury drugorzędowej białka możemy dokonać, korzystając z darmowego programu RasMol.2 Otwieramy plik ze strukturą, wybierając z menu File opcję Open. Zmianę sposobu wyświetlania struktury dokonujemy, korzystając z menu Display wybierając odpowiednią opcje (np.: Ribbons lub Wireframe), zaś zmianę kolorów elementów wyświetlanych dokonujemy wybierając którąś z opcję (np.: Chain) z menu Colours.
Oglądając i analizując strukturę hemoglobiny odpowiedz na następujące pytania:
- Z ilu podjednostek białkowych składa się hemoglobina?
- Jaka jest struktura szkieletu hemu -płaska czy wypukła?
- Z czym koordynują atomy żelaza występujące w białku (jakie to są aminokwasy, grupy)?
- Jakie struktury drugorzędowe występują w białku? -proszę skorzystać z programu RasMol.
[1] Ze względu na dużą ilość atomów w cząsteczce dokonujemy jedynie w tym ćwiczeniu analizy gotowej struktury białka po uzupełnieniu jej atomami wodoru.
[2] Więcej informacji oraz program można uzyskać na stronach: http://www.bernstein-plus-sons.com/software/rasmol/doc/rasmol.html
Ustalanie bezwzględnej konfiguracji R, S na podstawie wzorów przestrzennych
Ćwiczenie
Ustalanie bezwzględnej konfiguracji R, S na podstawie wzorów przestrzennych
Narysuj jedną z wybranych struktur1 lub pobierz strukturę w postaci pliku xyz która jest umieszczona na koncu dokumnetu. Zoptymalizuj układ metodą półempiryczną PM3. Posługując się modelem trójwymiarowym określ konfigurację R, S chiralnych atomów węgla, poprzez obracanie cząsteczki w odpowiednich kierunkach.
Opis określania konfiguracji R, S - zgodnej z konwencją Cahna-Ingolda-Preloga znajdziemy między innymi w książce R. T. Morrison, R. N. Boyd, Chemia Organiczna, PWN, W-wa, 1985, t. 1, str. 170-173.
Użytkownicy programu HyperChem mogą sprawdzić swoją odpowiedź wybierając z menu Display opcję Labels, a następnie w nowym oknie zaznaczając opcję Chirality.
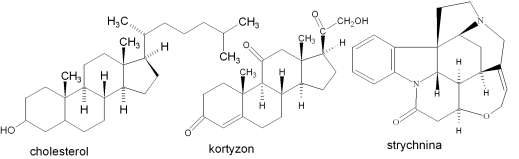
Cholesterol
6 12.127000000 -9.188000000 2.015000000
6 12.222000000 -10.488000000 1.238000000
6 9.738000000 -10.570000000 1.811000000
6 10.977000000 -11.387000000 1.386000000
6 8.469000000 -11.401000000 1.491000000
6 13.514000000 -8.621000000 1.722000000
6 10.984000000 -8.339000000 1.430000000
6 9.732000000 -9.191000000 1.105000000
6 13.562000000 -11.082000000 1.699000000
6 14.452000000 -9.828000000 1.908000000
6 11.171000000 -12.516000000 2.411000000
6 8.715000000 -12.913000000 1.798000000
6 9.814000000 -13.111000000 2.860000000
6 13.914000000 -7.438000000 2.638000000
6 11.883000000 -9.397000000 3.525000000
6 8.118000000 -11.267000000 0.000000000
6 7.302000000 -10.876000000 2.354000000
6 16.449000000 -7.552000000 2.339000000
6 15.169000000 -6.751000000 2.081000000
6 7.434000000 -13.655000000 2.244000000
6 12.806000000 -6.374000000 2.646000000
6 17.631000000 -6.774000000 1.752000000
6 5.979000000 -11.609000000 2.032000000
6 6.211000000 -13.050000000 1.544000000
1 12.298000000 -10.213000000 0.173000000
1 10.769000000 -11.831000000 0.395000000
1 9.765000000 -10.393000000 2.901000000
1 13.553000000 -8.285000000 0.666000000
6 18.959000000 -7.449000000 2.109000000
6 19.054000000 -8.840000000 1.471000000
6 20.111000000 -6.588000000 1.592000000
8 5.051000000 -13.832000000 1.780000000
1 11.306000000 -7.902000000 0.591000000
1 10.734000000 -7.637000000 2.097000000
1 8.919000000 -8.687000000 1.397000000
1 9.695000000 -9.339000000 0.117000000
1 13.944000000 -11.683000000 0.998000000
1 13.450000000 -11.592000000 2.552000000
1 14.844000000 -9.824000000 2.829000000
1 15.189000000 -9.802000000 1.232000000
1 11.647000000 -12.148000000 3.210000000
1 11.724000000 -13.238000000 1.996000000
1 9.021000000 -13.323000000 0.939000000
1 9.526000000 -12.662000000 3.706000000
1 9.928000000 -14.091000000 3.024000000
1 14.072000000 -7.796000000 3.558000000
1 12.531000000 -8.842000000 4.047000000
1 12.012000000 -10.362000000 3.753000000
1 10.949000000 -9.120000000 3.753000000
1 7.187000000 -10.912000000 -0.092000000
1 8.177000000 -12.163000000 -0.438000000
1 8.759000000 -10.636000000 -0.438000000
1 7.182000000 -9.899000000 2.177000000
1 7.524000000 -11.016000000 3.319000000
1 16.382000000 -8.447000000 1.899000000
1 16.579000000 -7.672000000 3.323000000
1 15.262000000 -5.855000000 2.514000000
1 15.060000000 -6.636000000 1.094000000
1 7.324000000 -13.566000000 3.234000000
1 7.507000000 -14.622000000 2.001000000
1 12.570000000 -6.147000000 3.591000000
1 11.998000000 -6.731000000 2.177000000
1 13.131000000 -5.553000000 2.177000000
1 17.627000000 -5.844000000 2.121000000
1 17.539000000 -6.739000000 0.757000000
1 5.496000000 -11.104000000 1.317000000
1 5.417000000 -11.638000000 2.858000000
1 6.330000000 -13.089000000 0.552000000
1 19.013000000 -7.545000000 3.103000000
1 19.101000000 -9.533000000 2.189000000
1 19.876000000 -8.890000000 0.904000000
1 18.246000000 -9.001000000 0.904000000
1 20.617000000 -6.209000000 2.367000000
1 19.745000000 -5.841000000 1.036000000
1 20.723000000 -7.150000000 1.036000000
1 4.572000000 -14.260000000 1.013000000
Kortyzon
6 10.500000000 -11.438000000 1.641000000
6 10.588000000 -12.956000000 1.425000000
6 9.206000000 -11.061000000 2.391000000
6 9.490000000 -13.736000000 1.457000000
6 7.971000000 -11.663000000 1.714000000
6 8.152000000 -13.160000000 1.694000000
6 13.041000000 -11.676000000 2.258000000
6 13.006000000 -12.516000000 0.974000000
6 11.690000000 -10.907000000 2.503000000
6 11.935000000 -13.601000000 1.163000000
6 14.058000000 -9.491000000 1.416000000
6 14.255000000 -10.725000000 2.262000000
6 13.049000000 -8.608000000 2.135000000
6 11.748000000 -9.383000000 2.265000000
6 15.468000000 -8.904000000 1.254000000
6 16.430000000 -10.072000000 1.539000000
6 15.546000000 -11.322000000 1.718000000
8 7.200000000 -13.882000000 1.886000000
6 10.483000000 -10.790000000 0.239000000
8 10.704000000 -8.776000000 2.171000000
1 11.432000000 -11.087000000 3.565000000
1 14.408000000 -10.390000000 3.304000000
1 15.593000000 -8.572000000 0.207000000
1 13.166000000 -12.387000000 3.094000000
6 13.547000000 -9.802000000 0.000000000
6 15.763000000 -7.731000000 2.169000000
8 15.181000000 -7.623000000 3.223000000
6 16.769000000 -6.686000000 1.748000000
8 17.922000000 -6.790000000 2.570000000
1 9.113000000 -10.066000000 2.403000000
1 9.259000000 -11.403000000 3.329000000
1 9.661000000 -14.710000000 1.310000000
1 7.887000000 -11.321000000 0.778000000
1 7.146000000 -11.431000000 2.230000000
1 13.898000000 -12.940000000 0.819000000
1 12.772000000 -11.937000000 0.193000000
1 11.875000000 -14.160000000 0.336000000
1 12.178000000 -14.180000000 1.941000000
1 12.894000000 -7.773000000 1.608000000
1 13.393000000 -8.371000000 3.044000000
1 16.953000000 -9.894000000 2.373000000
1 17.059000000 -10.199000000 0.771000000
1 15.387000000 -11.786000000 0.847000000
1 15.948000000 -11.965000000 2.371000000
1 10.458000000 -9.795000000 0.332000000
1 9.674000000 -11.099000000 -0.261000000
1 11.307000000 -11.057000000 -0.261000000
1 12.693000000 -10.319000000 0.060000000
1 14.231000000 -10.342000000 -0.490000000
1 13.384000000 -8.945000000 -0.490000000
1 16.390000000 -5.766000000 1.855000000
1 17.047000000 -6.824000000 0.798000000
1 18.815000000 -6.973000000 2.158000000
Strychnina
C -3.93272093 1.49162791 -1.41904651
C -4.39672093 0.18562791 -1.26604651
C -2.70772093 1.87862791 -0.88804651
C -3.64272093 -0.76337209 -0.58204651
C -1.97172093 0.92462791 -0.20904651
C -2.42572093 -0.36737209 -0.05604651
C -0.65272093 2.07962791 1.62895349
C -0.63772093 1.08762791 0.46895349
N -1.50272093 -1.16137209 0.67095349
C -0.26372093 -0.37737209 0.76795349
C 0.58927907 1.51462791 -0.23704651
C 0.83127907 1.12962791 -1.64604651
C 0.58627907 -1.02137209 -0.36604651
C 1.62727907 -0.09237209 -1.08404651
C 0.78827907 2.66062791 1.66095349
N 1.35527907 2.61062791 0.29495349
C -1.31872093 -2.63237209 0.84195349
C 1.17327907 -2.22237209 0.26895349
C 0.00227907 -3.23037209 0.19795349
C 2.70427907 0.37662791 -0.07004651
C 3.56327907 -0.51637209 0.45195349
O 2.33927907 -2.58137209 -0.46304651
C 3.55427907 -2.01637209 0.06795349
C 2.69427907 1.91062791 0.35395349
H 1.24927907 0.75262791 0.21195349
H 0.20327907 -0.46237209 1.76495349
H 1.46027907 -2.02637209 1.31895349
H 2.10427907 -0.64337209 -1.91604651
H -0.10272093 -1.35637209 -1.16504651
H -4.48572093 2.16062791 -1.91604651
H -5.28172093 -0.07437209 -1.65204651
H -2.36772093 2.81362791 -0.99004651
H -3.96672093 -1.70237209 -0.47104651
H -0.87072093 1.61162791 2.48495349
H -1.32672093 2.79962791 1.46195349
H 1.37227907 1.79262791 -2.16404651
H 0.00227907 0.90462791 -2.15604651
H 1.37127907 2.12162791 2.26895349
H 0.77727907 3.61262791 1.96695349
H -2.11672093 -3.06937209 0.42895349
H -1.31572093 -2.80637209 1.82695349
H -0.16572093 -3.45237209 -0.76304651
H 0.26827907 -4.05937209 0.68995349
H 4.18727907 -0.08137209 1.10095349
H 3.76627907 -2.56037209 0.87995349
H 4.24927907 -2.17737209 -0.63204651
H 3.01527907 1.98862791 1.29795349
H 3.30827907 2.41862791 -0.25104651
[1] W 1965 roku Robert Burns Woodward (USA) otrzymał Nagrodę Nobla za wybitne osiągnięcia w sztuce syntezy organicznej -for his outstanding achievements in the art of organic synthesis? za opracowanie między innymi syntezy cholesterolu, kortyzolu, strychniny, chlorofilu.
Konstruowanie cząsteczek
Ćwiczenie
Konstruowanie cząsteczek
Po zapoznaniu się z możliwościami programu GaussView, Molekel, ArgusLab, Gabedit lub HyperChem narysuj:
- odpowiednie cząsteczki na podstawie poniższych wzorów. Spróbuj pozmieniać kąty i długości wiązań w cząsteczkach tak, aby odpowiadały wzorom strukturalnym.
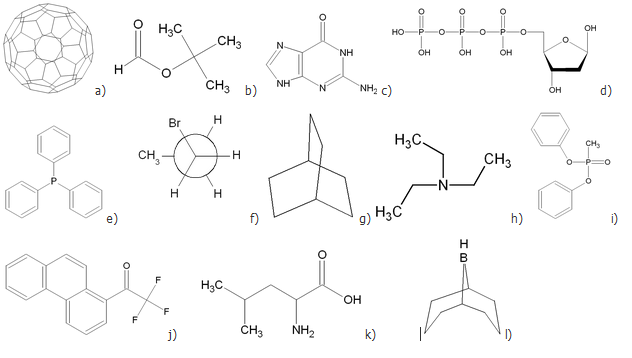
- ludzki hormon bradykininę, który jest odpowiedzialny za zmniejszanie ciśnienie krwi: Arg-Pro-Pro-Gly-Phe--Ser-Pro-Phe-Arg.
- skonstruuj wszystkie kodony glicyny: GGA, GGC, GGG.
- Dla wybranej cząsteczki z zadania pierwszego zmień: długość wiązania, wybrany kąt, oraz kąt dwuścienny.
Analiza struktury i trwałości karbokationów metodą ab initio
Ćwiczenie
Analiza struktury i trwałości karbokationów metodą ab initio
Karbokation to kation z ładunkiem dodatnim zlokalizowanym na atomie węgla. Atom węgla na którym zlokalizowany jest ładunek dodatni posiada tylko 6 elektronów i jest bardzo reaktywny - chętnie przyłączy anion (gdyż anion posiada dwa elektrony konieczne do utworzenia oktetu elektronowego). Stabilność karbokationu zależy od rzędowości atomu węgla - im wyższa tym bardziej trwały karbokation. Szczególnie trwałe są kationy allilowe (H2=CH-CH2+) i benzylowe (C6H5-CH2+), gdyż są dodatkowo stabilizowane przez rezonans wiązań wielokrotnych. Karbokationy powstają jako produkty pośrednie w wielu reakcjach chemicznych. Od ich trwałości zależy przebieg reakcji chemicznej i struktura powstałych produktów.
Ćwiczenie A
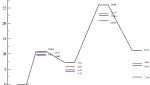
Uszereguj karbokationy ze względu na reaktywność na podstawie obliczenia energii reakcji addycji karbokationu do jonu chlorkowego: R+ + Cl- -> R-Cl przedstawione poniżej na schemacie karbokationy:
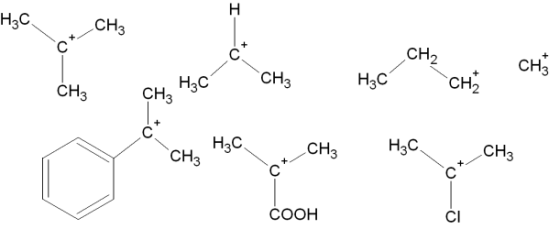
Do obliczenia energii reakcji zastosuj następującą zależność:
dletaEreakcji = deltaER+ + deltaECl- - deltaER-Cl
Otrzymane wyniki porównaj z wartościami empirycznymi oraz z trwałością karbokationów przedstawionych w książkach do chemii organicznej.
Ćwiczenie B
Na podstawie obliczenia energii poszczególnych produktu przejściowego addycji chlorowodoru do propenu wybierz odpowiedni produkt reakcji. Reakcja addycji do wiązania podwójnego biegnie poprzez powstawanie karbokationów.

możliwe produkty pośrednie
Określ różnice energii pomiędzy dwoma możliwymi karbokationami w tej reakcji. Porównaj otrzymany wynik z regułą Markownikowa z 1869. *Wytłumacz regułę Zajcewa sformułowaną w 1875 roku.
Macierz-Z
Ćwiczenie
Macierz-Z
1. Korzystając z informacji zawartych w serwisie molnet eu zbuduj macierz-Z dla cząsteczek: a) NH3, H2S, CH4, eten, CO2, glioksal
b) PH3, H2O, NH4+, aldehyd mrówkowy, acetylen.
2. Na podstawie macierzy-Z określ strukturę związku i nazwij go:
a)
N
H 1 B1
C 1 B2 2 A1
H 1 B3 3 A2 2 D1
H 1 B4 3 A3 2 D2 C 3 B5 1 A4 4 D3
H 3 B6 1 A5 6 D4
H 3 B7 1 A6 6 D5
O 6 B8 3 A7 1 D6
O 6 B9 3 A8 1 D7
B1 1.05630001
B2 1.48267023
B3 1.01531449
B4 1.01531449
B5 1.59440210
B6 1.11879807
B7 1.11879807
B8 1.26201665
B9 1.23972237
A1 105.38751147
A2 111.60873785
A3 111.60873785
A4 109.91889354
A5 109.97608441
A6 109.97608441
A7 114.41315293
A8 115.11851910
D1 -118.41489861
D2 118.41489861
D3 -118.41489861
D4 119.31520186
D5 -119.31520186
D6 0.00000000
D7 180.00000000
b)
N
C 1 1.370000
H 2 1.080000 1 120.000018
C 2 1.339999 1 121.220045 3 177.300027 D1
H 4 1.089999 2 120.000084 1 -180.000000 D2
C 4 1.439999 2 120.780053 1 0.000000 D3
O 6 1.230000 4 125.350088 2 -180.000000 D4
N 6 1.380000 4 114.070089 2 0.000000 D5
H 8 1.089999 6 116.770091 4 -180.000000 D6
C 1 1.370182 2 122.209093 4 0.000000 D7
O 10 1.220000 1 123.039216 2 180.000000 D8
H 1 1.000000 2 118.895453 4 180.000000 D9
Moment dipolowy cząsteczki
Ćwiczenie
Moment dipolowy cząsteczki
Moment dipolowy towarzyszy cząsteczkom, w których występuje nierównomierne i niesymetrycznie rozłożony ładunek. Opisuje on pośrednio "wypadkowe rozłożenie ładunku" i charakteryzuje bezpośrednio dipol. Duży wpływ na wielkość momentu dipolowego ma elektroujemność pierwiastków oraz geometria cząsteczki. Tak na przykład woda dzięki budowie kątowej posiada moment dipolowy a dwutlenek węgla już nie, ponieważ posiada budowę liniową. Moment dipolowy jest wartością wektorową, a cząsteczki posiadające trwały, niezerowy moment dipolowy nazywamy polarnymi. Wartość wektora momentu dipolowego możemy policzyć z obliczonego rozkładu ładunków Mullikena, podstawiając do wzoru:
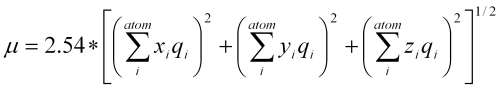
Wartość otrzymujemy w Debay'ach, a x, y, z są współrzędnymi kartezjańskimi ładunków.
więcej informacji także w artykule Moment dipolowy
Obliczenia momenty dipolwego w programie Gaussianie
Obliczenia momentu dipolowego, jak i rozkład ładunków jest liczony standardowo za każdym razem podczas obliczeń. Po skończeniu obliczeń wartości momentów dipolowych w pliku wynikowym możemy znaleźć na samym końcu po słowie Dipole=.
1\1\ WCSS-GROMADA-COMPUTE-1-6\SP\RB3LYP\6-31G(d,p)\H2O1\MAREKDOS\10-Ma
y-2007\0\\#P B3LYP/6-31G(D,P) SCRF=(CPCM,SOLVENT=WATER,READ) GEOM=CHEC
KPOINT\\Title Card Required\\0,1\O,0,-0.0954094714,0.,-0.072620685\H,0
,-0.079238472,0.,0.8959847601\H,0,0.8425142434,0.,-0.3150192802\\Versi
on=IA64L-G03RevC.02\State=1-A'\HF=-76.4309029\RMSD=2.134e-05\Dipole=0.
7374232,0.0,0.5612878\PG=CS [SG(H2O1)]\\@
NO SCIENCE HAS EVER MADE MORE RAPID PROGRESS IN A
SHORTER TIME THAN CHEMISTRY.
-- MARTIN HEINRICH KLOPROTH, 1791
(FIRST PROFESSOR OF CHEMISTRY AT THE UNIVERSITY OF BERLIN)
Job cpu time: 0 days 0 hours 0 minutes 3.7 seconds.
File lengths (MBytes): RWF= 17 Int= 0 D2E= 0 Chk= 10 Scr= 1
Normal termination of Gaussian 03 at Thu May 10 11:12:07 2007.
Podstawiając trzy kolejne liczby zaznaczone pogrubieniem do wzoru: μ=2.54.(x2 + y2 + z2)1/2 otrzymujemy moment dipolowy w Debay'ach.
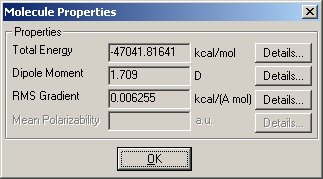
Można także skorzystać z programu GaussView. Z zakładki Results wybieramy Summary i otrzymujemy już wyliczoną wartość momentu dipolowego.
Obliczanie momentu dipolowego z wykorzystaniem programu HyperChem
CCl4, CHCl3, CH2Cl2, CHCl3, CCl4, benzen, fenol, alanina, H2O, H3O+, 2-chloropropan, 1,4-dioksan

Odpowiedz na pytania:
Jak symetria wpływa na moment dipolowy?
Czy któraś z konformacji 1,4-dioksanu przeważa w warunkach normalnych?
Która z baz lepiej nadaje się do obliczeń wartości momentu dipolowego?
Jak wpływa moment dipolowy na polarność rozpuszczalników?
Jakimi wymienione substancje są rozpuszczalnikami polarnymi czy nie polarnymi?
Dla 1,4-dioksanu przeanalizuj izomery konformacyjne (podobne izomery są jak dla cykloheksanu).
Nano-ludziki bardziej rzeczywisty kształt
Ćwiczenie
Nano-ludziki bardziej rzeczywisty kształt
Czasami chemicy, syntezując różne związki chemiczne, wykazują się fantazją, otrzymując cząsteczki przypominające swoim kształtem na przykład "ludziki". W 2003 roku została opublikowana praca Chanteau i Tour[1] dotycząca struktur, które w schematach mają kształty antromorficzne:

Dla wybranego "ludzika" skonstruuj model przestrzenny oraz przeprowadź optymalizację cząsteczki metodą AM1 i odpowiedz na pytania:
a) Czy kształt przedstawiony schematycznie odpowiada twoim obliczeniom?
b) Jakie nazwy posiadają według autorów wymienionej publikacji "ludziki" na schemacie?
c) Czy można w literaturze spotkać podobne przypadki "ciekawej syntezy"?
1 Chanteau, S. H.; Tour, J. M., Synthesis of Anthropomorphic Molecules: The NanoPutians. J. Org. Chem. 2003, 68, (23), 8750-8766
Strona 2 z 4