Kwasowość Brønsteda
Dawid Gąszowski
Wstęp
Równowagi kwasowo - zasadowe składają się na podstawy chemii. Szczególnego znaczenia nabiera kwasowość ciągle powiększającej się grupy związków o charakterze superkwasowym. Tego typu związki znajdują zastosowanie jako katalizatory. Wiele z nich, np. klatki karboranowe, cz y zeolity to ciała stałe, więc "klasyczne" definicje kwasowości oparte o pH, czy funkcję kwasowości Hammet'a są bezużyteczne. Stąd konieczność obliczeń.
To opracowanie ma na celu pokazać sposób opisu kwasowości w fazie gazowej za pomocą chemii obliczeniowej.
Reakcja protonowania
Reakcja protonowania zasady B w fazie gazowej jest dana równaniem:
- Bn-1(g) + H+(g) → BHn(g)
Deskryptorem kwasowości w chemii obliczeniowej jest powinowactwo protonowe zasady B zdefinowane następująco w fazie gazowej:
- PA(Bn-1)=ΔEel + Δ(ZPVE) + ΔEt + ΔEr + ΔEv + Δ(pV)
- ΔEel = [ Etot(Bn-1) + Etot(H+) - Etot(BH)]
Na powyższe równania składa się różnica całkowitych energii substratów i produktów reakcji protonowani - ΔEel , różnica energii punktów zerowych reagentów, Δ(ZPVE), różnice energii wynikające ze zmiany liczby translacyjnych, rotacyjnych i oscylacyjnych stopni swobody - ΔEt,r,v . Wszystko to złożone razem daje ujemną standardowa entalpię reakcji protonowania w fazie gazowej.
Podział trichotomiczny
Powinowactwo protonowe jest doskonałą wielkością do korelacji z eksperymentem, nie oddaje jednak mechanizmu procesu protonowania. Proces ten można przedstawić za pomocą reakcji:
- AH - H+ = A- - PA(A-) (R1)
- A• + e- = A- + EA(A•) (R2)
- A• + H• = AH + (BAE)•AH (R3)
- H+ + e- = H• + EA(H+) (R4)
Deprotonację można rozumieć na dwa sposoby:
-
heterolityczny rozpad wiązania (R1)
-
homolityczny rozpad wiązania (R3), a następnie transfer elektronu z atomu wodoru do obojętnego rodnika A• z utworzeniem jonu A- i protonu (R2 i odwrócona R4)
Efekty energetyczne obu procesów są jednakowe. Drugie podejście pozwala jednak wyrazić znane już nam powinowactwo protonowe w nieco odmiennej formie:
- PA(A-) = -EA(A•) + EA(H+) + (BAE)•AH
Pierwszym składnikiem równania jest ujemne powinowactwo elektronowe obojętnego rodnika A•, czyli efekt energetyczny przeniesienia elektronu z atomu wodoru na ów rodnik - jest to pierwszy etap protonowania. Równocześnie elektron musi zostać z atomu wodoru "oderwany". Jest to uzwględnione w członie EA(H+) - powinowactwie elektronowym protonu. Następnie tworzy się wiązanie pomiędzy parą rodników A• i H•, czemu odpowiada ostatni wyraz równania. Znaki poszczególnych wkładów energetycznych są zamienione (energia asocjacji wiązania powinna być przecież ujemna) dlatego, że odnosimy się do zasady (A-, powinowactwo protonowe) a nie do kwasu (AH, kwasowość). Jak obliczyć człony równania? Powinowactwo elektronowe protonu to stała, z tym nie ma problemu. Wiadomo też czym jest energia asocjacji wiązania, BAE. Powinowactwo elektronowe rodnika A• odpowiada natomiast adiabatycznemu pierwszemu potencjałowi jonizacji jonu A- - IP(A-)AD1. Jest to najmniejsza energia potrzebna do oderwania elektronu z tego jonu. Można teraz napisać:
-
PA(A-) = -IP(A-)Koopn + E(ei) + (BAE)•AH + 313.6
-
E(ei) = -IP(A-)Koopn + IP(A-)AD1
Widać, że pierwszy i drugi człon kompensują się pozostawiają adiabatyczny potencjał jonizacji. -IP(A-)Koopn to wertykalny potencjał jonizacji, obliczony na podstawie twierdzenia Koopmansa, przy założeniu, że geometria cząsteczki w procesie jonizacji nie zmienia. Pozostaje on we wzorze ze względów interpretacyjnych.
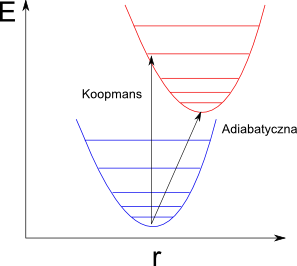
Rysunek przedstawia schematycznie różnicę pomiędzy wertykalną i adiabatyczną energią jonizacji dla cząsteczki dwuatomowej w przybliżeniu harmonicznym (za Computational Chemistry Comparison and Benchmark Database).
Kilka słów o potencjałach
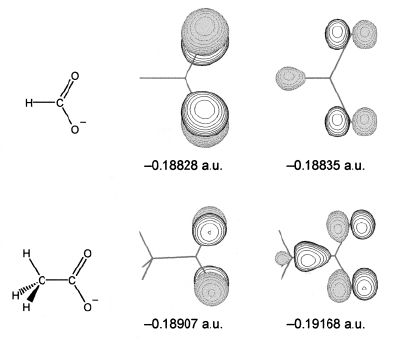
Potencjał jonizacji Koopmansa, odpowiada energii n - tego orbitalu molekularnego. W przypadku adiabatycznym jest to pierwszy potencjał jonizacji. Skąd ta rozbieżność? Trzeba pamiętać, że reakcje (de)protonowania zachodzą w pewnym określonym miejscu cząsteczki. Szukamy orbitalu, który jest zlokalizowany w miejscu protonowania. Przykładowo wiadomo, że w kwasach karboksylowych protonowanie zachodzi w płaszczyźnie grupy karboksylanowej. Orbital HOMO w tych związkach jest utworzony z orbitali π atomów tlenu. W takim przypadku za potencjał Koopmansa podstawimy energię orbitalu HOMO-1. Tego typu orbitale nazywa się PRIMO - PRIncipal Molecular Orbital. Na poniższym rysunku widać porównanie orbitali HOMO i PRIMO anionów kwasów mrówkowego i octowego:
Jak liczyć?
Liptak i Shields zrobili przegląd metod DFT w obliczeniach termochemicznych. Testowali 11 funkcjonałów na grupie 17 reakcji deprotonacji. Wyniki porównali z danymi zaczerpniętymi z bazy danych NIST, gdzie błąd pomiarowy jest mniejszy niż 1 kcal/mol. Najniższym odchyleniem standardowym wykazały się funkcjonały PBE1PBE (1.6 kcal/mol) oraz B3PW91 (1.9 kcal/mol). Dokładność taką otrzymano w bazie aug-cc-pVTZ użytej przy optymalizacji i obliczeniach częstości. Nieco starsze porównanie metod DFT wskazuje również na funkcjonał B3PW91 jako dający wyniki porównywalne z metodą G2 w grupie 32 związków. Często używany do obliczeń kwasowości jest wszędobylski B3LYP.
- W szczególny sposób trzeba podejść do obliczeń potencjałów jonizacji. Używając DFT natkniemy się na błędy wynikające ze złego zachowania się potencjału korelacyjno - wymiennego przy dużych odległościach od jądra (przypadek elektronu odrywanego od cząsteczki podczas jonizacji). Rozwiązaniem może być np. potencjał modelowy SAOP (od. Statistical Average of Orbital Potentials). Inne wyjście to zastosowanie DFT zależnej od czasu albo "ręczna" korekcja wartości potencjału o dane doświadczalne (najniższa energia jonizacji, którą trzeba dysponować).
- Mówiąc o obliczeniach kwasowości nie sposób nie wspomnieć o metodach kompozytowych (G1 – G5) i metodach typu Complete Basis Set oferowanych przez program Gaussian, a zaprojektowanych do bardzo dokładnych obliczeń energii. Dokładność jednak ma swoją cenę i metody te mogą być używane do niezbyt dużych układów. Jak wspomniano wcześniej, niektóre funkcjonały mogą dać porównywalną jakość wyników niższym kosztem.
- Obliczenia potencjałów Koopmansa z definicji wykonuje się metodą Hartree-Focka w dużej bazie funkcyjnej.