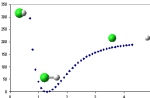
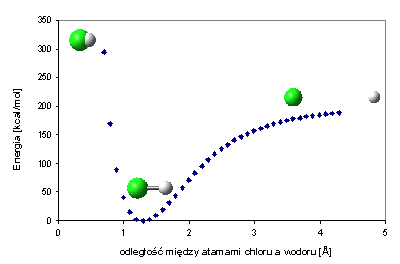
 Mając najprostszą cząsteczkę dwuatomową wiemy, że istnieje pewna optymalna odległość między atomami gdzie energia układu jest najmniejsza. Odległość tą nazywamy długością wiązania. Możemy ją obliczyć poprzez obliczanie energii dla kolejnych odległości między atomami. W ten sposób możemy sporządzić wykres zależności energii od odległości między atomami. W takim przypadku uzyskaną krzywą nazywamy krzywą energii potencjalnej. Minimum energii odpowiada geometrii, w której cząsteczka występuje w stanie stacjonarnym, to znaczy w badanym medium ilość cząsteczek o danej geometrii jest największa.
Mając najprostszą cząsteczkę dwuatomową wiemy, że istnieje pewna optymalna odległość między atomami gdzie energia układu jest najmniejsza. Odległość tą nazywamy długością wiązania. Możemy ją obliczyć poprzez obliczanie energii dla kolejnych odległości między atomami. W ten sposób możemy sporządzić wykres zależności energii od odległości między atomami. W takim przypadku uzyskaną krzywą nazywamy krzywą energii potencjalnej. Minimum energii odpowiada geometrii, w której cząsteczka występuje w stanie stacjonarnym, to znaczy w badanym medium ilość cząsteczek o danej geometrii jest największa.
Oczywiście jest to pewne uproszczenie dlatego, że cząsteczka ciągle drga, co wiąże się z niewielką zmianą energii. Zależność energii od odległości między dwoma atomami związana jest z oddziaływaniem elektronów prowadzących do powstania wiązania. Różnica energii między cząsteczką w minimum a fragmentami cząsteczki oddalonymi w nieskończoności jest energią dysocjacji wiązania. Niestety nie wszystkie metody stosowane do obliczeń dają poprawne wyniki podczas obliczania energii dysocjacji takim sposobem. Metody Hartree Fock[1] dają najgorsze wyniki, z metod ab-initio lepsze wyniki dają metody DFT, a najlepsze metody wielo wyznacznikowe.
Dla cząsteczek wieloatomowych minimum energii zależy od ułożenia i oddziaływania wszystkich atomów między sobą. Aby wyznaczyć minimum, o najmniejszej energii musimy w obliczeniach uwzględnić wszystkie atomy. Dla prostych cząsteczek dwu, trzy atomowych możemy poprzez zadawanie kolejnych wartości odległości oraz kątów dojść do struktury o najniżej energii. Dla cząsteczek bardziej skomplikowanych musimy posłużyć się pewnymi algorytmami znajdującymi geometrię cząsteczki o najmniejszej energii całkowitej - ten proces nosi nazwę optymalizacji cząsteczki i prowadzi do minimum energetycznego dla układu.
Jeżeli dany układ składa się z więcej niż z dwóch atomów, może mieć kilka różnych minimów. Postaramy się to z ilustrować na przykładzie analizy konformacyjnej cząsteczki 1-chloropropanu dla którego zmieniano kąt torsyjny - między atomami Cl-C-C-C o jeden stopień.

Rysunek 1-chloropropanu zaznaczonym katem - o wartości 180° który będziemy zmieniać
Po zamrożeniu kąta - prowadzono optymalizacje cząsteczki i obliczano jej energie.2 Proces ten popularnie nazywamy: "skanem z relaksacją". Uzyskano następującą krzywą energii potencjalnej:

Wykres energii potencjalnej dla ścieżki zmiany konformacji 1-chloropropanu
Na wykresie możemy zauważyć, że dla pewnych konformerów wartość energii potencjalnej osiąga minima, minimum najgłębsze nazywamy minimem globalnym zaś pozostałe nazywamy lokalnymi. Podobnie jest z maksimami.
Startując z rożnych struktur 1-chloropropanu różniących się jedynie kątem dwuściennym, możemy zoptymalizować cząsteczkę do dwóch minimów lokalnych oraz do jedno globalnego w zależności, z jakiej wartości kąta dwuściennego starujemy oraz jakiego algorytmu optymalizującego używamy. Dlatego podczas optymalizacji warto zwracać uwagę na ewentualne izomery geometryczne. Struktura cząsteczki o najmniejszej energii jest strukturą, której populacja jest największa. Jednak przy niektórych cząsteczkach np.: przy długich polimerach o strukturze najbardziej prawdopodobnej decyduje oprócz energii cząsteczki także i prawdopodobieństwo występowania danej struktury (np.: zgięcie łańcucha w polimerach). Jeżeli mamy większą liczba parametrów (już przy trzech atomach mamy dwie odległości i jeden kąt), których wartości możemy zmieniać, wówczas uzyskujemy płaszczyznę wielowymiarową. Dla trzech zmiennych możemy przedstawić zależność energii od parametrów na wykresie trójwymiarowym: Wykresy takiego typu są graficznym przedstawieniem za pomocą powierzchni zależności energii potencjalnej od parametrów geometrycznych (z ang. PES -Potential Energy Surface). 3

Na płaszczyźnie przedstawionej na wykresie pojawiają się nam dodatkowe charakterystyczne punkty ? minima w ekstremach funkcji ? tak zwane punkty siodłowe.4
Od zoptymalizowanej struktury cząsteczki zależą wartości wyliczone w następnych krokach bazujące na geometrii cząsteczki, dlatego należy dokładnie przeprowadzić optymalizację i znaleźć minimum globalne. Dokładność optymalizacji zależy od wybranego algorytmu oraz opcji optymalizacji. Zgodność zaś teoretycznego modelu z rzeczywistym zależy od metody obliczeniowej, bazy i na przykład od uwzględnienia oddziaływania z rozpuszczalnikiem.5 Dla dużych cząsteczek przeważnie stosuje się początkową optymalizację w prostych metodach i w małych bazach. Po wstępnej optymalizacji cząsteczki przeprowadza się optymalizację dokładniejszymi metodami z rozbudowanymi bazami. Różnica wyliczonej geometrii oraz energii pomiędzy różnymi metodami i bazami wynika ze sposobu opisu kwantowego cząsteczek - dlatego zestawiając obliczenia i porównując je, powinniśmy stosować te same bazy i metody. Porównując dwie cząsteczki w dwóch minimach, stosujemy różnice energii między nimi. Wyliczone energie układu i geometrie mają sens jedynie w maksimach lub w stanach przejściowych - punktach siodłowych, o czym będzie mowa w następnych rozdziałach.
Przypisy:
1 Dokładne wytłumaczenie tego problemu można znaleźć na stronie 378 książki Idee Chemii Kwantowej Lucjana Pieli, PWN 2003, bądź w innych podręcznikach do chemii kwantowej
2 Gaussian03, metoda AM1 - wybór metody do przedstawienia przykładu nie jest istotny.
3 Wykres wykonany w programie Origin 7.0
4 W terminologii angielskiej: saddle point.
5 Programy w standardowo zakładają optymalizację w próżni. Można jednak przeprowadzić ją z uwzględnieniem rozpuszczalnika i odpowiedniego modelu rozpuszczalnika.