Obliczanie energii oddziaływania

Obliczanie energii oddziaływania

Pierwszym etapem obliczeń energii oraz sposobów oddziaływania jest optymalizacja kompleksu cząsteczek. Należy tak zbudować cząsteczki i tak ustawić je koło siebie, żeby jak najlepiej odzwierciedlały możliwe oddziaływania. Następnie taki układ poddajemy procesowi optymalizacji. Czasami do końca nie wiemy, w którym miejscu następuje oddziaływanie wówczas próbujemy różnych sposobów.

Jeżeli otrzymaliśmy zoptymalizowany kompleks dwóch cząsteczek, wówczas przystępujemy do analizy wiązań wodorowych (odległości, kąty) lub do klasyfikacji występujących oddziaływań. Tą analizę opieramy na strukturze kompleksu. Jednym z ważniejszych parametrów są obliczenia energii. Załóżmy, że nasz kompleks składa się z dwóch fragmentów: A i B. Jeżeli znamy energie zoptymalizowanych osobno fragmentów A i B oraz energię kompleksu, wówczas możemy obliczyć energię dysocjacji kompleksu. Liczona jest ona jako różnica energii kompleksu AB i osobno fragmentów A i B. Można to wyrazić wzorem:

ΔE_dysocjacji = E_AB – E_A’ – E_B'

Kolejną energię, którą możemy obliczyć to energia oddziaływania. Energia oddziaływania jest różnicą energii kompleksu E_AB i sumy energii poszczególnych fragmentów wchodzących w skład tego kompleksu.

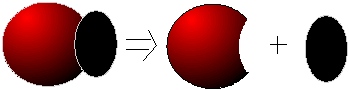
ΔE_oddzial = E_AB – (E_A + E_B)

Energie poszczególnych fragmetów A i B są liczone dla geometrii takiej samej jaką posiadają te fragmenty w kompleksie. Należy wspomnieć, że energia kompleksu jest liczona z zastosowaniem bazy AB, zaś energia poszczególnych fragmentów – w bazach tych fragmentów (E_A w bazie A i E_B w bazie B, rysunek powyżej). W takim podejściu obliczona energia zawiera błąd związany z rozmiarem bazy funkcyjnej dla podukładów A i B. Rozszerzenie bazy dla podukładów A oraz B o bazę funkcyjną całego kompleksu AB wiąże się z obniżeniem energii tych fragmentów i lepsze zbliżenie do wartości oczekiwanych. Błąd ten nazywa się błędem superpozycji bazy BSSE. Błąd superpozycji bazy, zgodnie ze schamatem zaproponowanym przez Boysa i Bernardiego, jest to różnica sumy energii substratów liczonych w pełnej bazie AB i sumy energii substratów liczonych osobno: E_A w bazie A i E_B w bazie B.

BSSE = (E_AB + E_AB) – (E_A + E_B)

Chcąc obliczyć energię oddziaływania kompleksu z uwzględnieniem BSSE, od energii kompleksu AB liczonego w bazie AB trzeba odjąć sumę energii podukładu A liczonego w bazie AB i podukładu B liczonego w bazie AB rysunek poniżej:

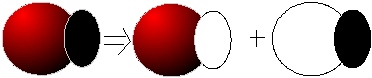
ΔE_oddzial^BSSE = E_AB – (E_A(AB) + E_B(AB))

Ukazany powyżej sposób obliczeń nie jest trudny do przeprowadzenia. Do obliczeń wybierzmy kompleks chlorowodoru z cząsteczką wody (H₂O:HCl). W pierwszym etapie optymalizujemy kompleks oraz obliczamy częstości, żeby sprawdzić czy kompleks jest w minimum energetycznym. Plik obliczeń (h2ohcl.inp) wygląda następująco:

%chk=h2ohcl.chk
%nproc=2
%mem=1500mb
# opt freq b3lyp/6-31G(d)

kompleks H₂O z HCl

0 1
O 0.448141 0.316244 0.198285
H 0.480086 -0.077493 1.083718
H 1.167086 -0.111305 -0.292018
H -1.108258 -0.165684 -0.494586
Cl -2.260912 -0.606682 -0.977408

Następnie sprawdzamy częstości, jeżeli wszystkie są  dodatnie, to przechodzimy dalej do obliczeń. Za pomocą programu Molden wczytujemy plik z wynikami h2ohcl.log. Przechodzimy do ostatniego kroku optymalizacji.

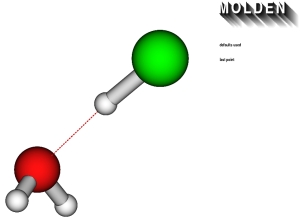
5
scf done: -537.218903
O 0.448728 0.324467 0.209110
H 0.497205 -0.076345 1.091713
H 1.136485 -0.127585 -0.305288
H -1.114323 -0.146537 -0.489077
Cl -2.241953 -0.618921 -0.988466

%chk=h2ohcl_BSSE.chk
%nproc=2
%mem=1500mb
# counterpoise=2 b3lyp/6-31G(d)

kompleks H2o z HCl obliczenie bledu superpozycji bazy

0 1, 0 1, 0 1
O 0.448728 0.324467 0.209110 1
H 0.497205 -0.076345 1.091713 1
H 1.136485 -0.127585 -0.305288 1
H -1.114323 -0.146537 -0.489077 2
Cl -2.241953 -0.618921 -0.988466 2

Pierwsza linia SCF Done reprezentuje energię całej cząsteczki.

There are    40 symmetry adapted basis functions of A   symmetry.
 Integral buffers will be    131072 words long.
 Raffenetti 2 integral format.
 Two-electron integral symmetry is turned on.
    40 basis functions,    92 primitive gaussians,    40 cartesian basis functions
    14 alpha electrons       14 beta electrons
       nuclear repulsion energy        47.1715240149 Hartrees.
 NAtoms=    5 NActive=    5 NUniq=    5 SFac= 1.00D+00 NAtFMM=   60 Big=F
 One-electron integrals computed using PRISM.
 NBasis=    40 RedAO= T  NBF=    40
 NBsUse=    40 1.00D-06 NBFU=    40
 Harris functional with IExCor=  402 diagonalized for initial guess.
 ExpMin= 1.43D-01 ExpMax= 2.52D+04 ExpMxC= 3.78D+03 IAcc=1 IRadAn=         1 AccDes= 1.00D-06
 HarFok:  IExCor= 402 AccDes= 1.00D-06 IRadAn=         1 IDoV=1
 ScaDFX=  1.000000  1.000000  1.000000  1.000000
 Initial guess orbital symmetries:
       Occupied  (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
                 (A) (A)
       Virtual   (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
                 (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
                 (A) (A)
 The electronic state of the initial guess is 1-A.
 Warning!  Cutoffs for single-point calculations used.
 Requested convergence on RMS density matrix=1.00D-04 within 128 cycles.
 Requested convergence on MAX density matrix=1.00D-02.
 Requested convergence on             energy=5.00D-05.
 No special actions if energy rises.
 Keep R1 integrals in memory in canonical form, NReq=     1255471.
 SCF Done:  E(RB+HF-LYP) =  -537.218903306     A.U. after    6 cycles
             Convg  =    0.5621D-05             -V/T =  2.0038
             S**2   =   0.0000

Druga linia SCF Done reprezentuje fragment pierwszy w bazie dimer, należy zwrócić uwagę na fragment poprzedzający SCF Done, kilka lini wyżej jest użyty skrót DCBS – oznacza to, że obliczenia wykonywane są w bazie dimeru.

 Counterpoise: doing DCBS calculation for fragment   1 NewBq=T
 Basis read from rwf:  (6D, 7F)
 There are    40 symmetry adapted basis functions of A   symmetry.
 Integral buffers will be    131072 words long.
 Raffenetti 2 integral format.
 Two-electron integral symmetry is turned on.
    40 basis functions,    92 primitive gaussians,    40 cartesian basis functions
     5 alpha electrons        5 beta electrons
       nuclear repulsion energy         9.0679564666 Hartrees.
 NAtoms=    5 NActive=    5 NUniq=    5 SFac= 1.00D+00 NAtFMM=   60 Big=F
 One-electron integrals computed using PRISM.
 NBasis=    40 RedAO= T  NBF=    40
 NBsUse=    40 1.00D-06 NBFU=    40
 Harris functional with IExCor=  402 diagonalized for initial guess.
 ExpMin= 1.43D-01 ExpMax= 2.52D+04 ExpMxC= 3.78D+03 IAcc=1 IRadAn=        
 1 AccDes= 1.00D-06
 HarFok:  IExCor= 402 AccDes= 1.00D-06 IRadAn=         1 IDoV=1
 ScaDFX=  1.000000  1.000000  1.000000  1.000000
 Initial guess orbital symmetries:
       Occupied  (A) (A) (A) (A) (A)
       Virtual   (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
                 (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
                 (A) (A) (A) (A) (A) (A) (A) (A) (A) (A) (A)
 The electronic state of the initial guess is 1-A.
 Warning!  Cutoffs for single-point calculations used.
 Requested convergence on RMS density matrix=1.00D-04 within 128 cycles.
 Requested convergence on MAX density matrix=1.00D-02.
 Requested convergence on             energy=5.00D-05.
 No special actions if energy rises.
 Keep R1 integrals in memory in canonical form, NReq=     1255471.
 SCF Done:  E(RB+HF-LYP) =  -76.4113995017     A.U. after    5 cycles
             Convg  =    0.4853D-05             -V/T =  2.0083
             S**2   =   0.0000

Trzecia linia SCF Done odpowiada energii drugiego fragmentu w bazie dimeru.

Counterpoise: doing DCBS calculation for fragment 2 NewBq=T
.
.
SCF Done: E(RB+HF-LYP) = -460.795541716 A.U. after 4 cycles
Convg = 0.1717D-04 -V/T = 2.0031
S**2 = 0.0000

Czwarta linia SCF Done informuje o energii fragmentu pierwszego obliczony w swojej bazie (monomeru). Użyty jest skrót MCBS.

Counterpoise: doing MCBS calculation for fragment 1
.
.
Keep R1 integrals in memory in canonical form, NReq= 885565.
SCF Done: E(RB+HF-LYP) = -76.4089088740 A.U. after 5 cycles

Piąta linia SCF Done informuje nas o energii drugiego fragmentu w swojej bazie.

Counterpoise: doing MCBS calculation for fragment 2
.
.
SCF Done: E(RB+HF-LYP) = -460.795172630 A.U. after 4 cycles

Counterpoise: corrected energy = -537.216043592858
Counterpoise: BSSE energy = 0.002859713284

Mając te wszystkie dane można policzyć energię oddziaływania z uwzględnieniem superpozycji bazy:

Możemy także obliczyć sam bład superpozycji bazy:

BSSE = E_A(DCBS) + E_B(DCBS) – (E_A(MCBS) + E_B(MCBS))

Energia wyliczona powinna się zgadzać z wyliczoną wartością corrected energy.

Obliczona energia oddziaływania dla naszego przykładu H₂O:HCl wynosi -0.01196 Hartree, czyli 7.50 kcal/mol, błąd superpozycji bazy wynosi 1.79 kcal/mol.

Ćwiczenie

Oblicz energię oddziaływania, z uwzględnieniem BSSE, dla dimeru wody. Podaj w komentarzach twoją wyliczoną wartość w kcal/mol. Wybierz jedną z podanych poniżej metod. Swoje wyniki umieść w komentarzu. Dodatkowo możesz napisać czas jaki był potrzeby do obliczeń BSSE. Po wykonaniu ćwiczenia przez kilka osób można porównać dokładność metod oraz czas jaki jest potrzebny z przeprowadzenia obliczeń.

AM1
B3LYP/6-31G(d)
B3LYP/6-31G(d,p)
B3LYP/6-31++G(d,p)
MP2/6-31G(d)
MP2/6-31G(d,p)