Praktyczna szkoła Modelowania I – 2009 - organizowana była wraz z ICM, pierwsza szkoła (22 osoby) zagadnienia z Gaussian, Hyperchema, oraz z innych programów modelowania.
Idea praktycznej Szkoły Modelowania Molekularnego narodziła się w wakacje 2009 roku. Była zainspirowana pobytem w Stanach Zjednoczonych w 2005 roku i uczestnictwem w szkoleniu organizowanym przez profesora Jerzego Leszczyńskiego, które odbyło się w Jackson State University. Zdobywanie wiedzy w Praktycznej Szkole Modelowania Molekularnego polega na rozwiązywaniu określonych problemów badawczych -rozwiązując je, uczestnik zdobywa informacje o narzędziach, a przede wszystkim o sposobie rozwiązania. Organizacja nauki takim sposobem jest trudniejsza, ale zamierzenie, jakim jest nauka analitycznego myślenia, rozwiązywania poprzez analogię, dedukcję, indukcję, abdukcję wydaje się o wiele cenniejsza niż sama wiedza z danej dziedziny. Dlatego stworzyliśmy szkołę łączącą wiedzę z dziedziny modelowania molekularnego wraz z praktycznym rozwiązywaniem problemów z dziedziny chemii, nanotechnologii, biotechnologii. Szkoła opiera się na pierwszym w Polsce serwisie internetowym do modelowania molekularnego i nie tylko: molnet.eu
Poniżej przedstawiamy dokumenty, informację już archiwalne związane z tą szkołą. Niektóre zagadnienia zostały poprawione i dołączone do kategorii szczegółowych serwisu molnet.eu
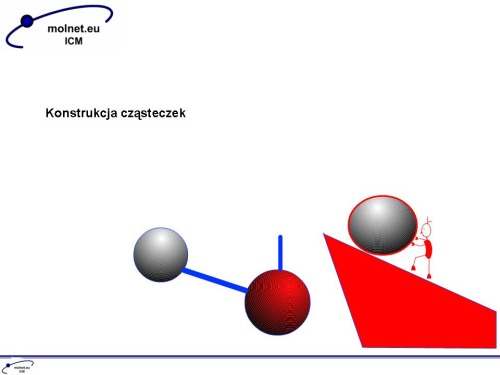
Jedną z podstawowych umiejętności, które musimy zdobyć, aby zacząć modelowanie, jest sprawna konstrukcja cząsteczek oraz układów tak, aby odzwierciedlały nasze zamierzenia. W szczególności istotne jest, to kiedy poszukujemy stanu przejściowego i korzystamy z algorytmu, w którym musimy podać hipotetyczny stan przejściowy (qst3).
Do konstrukcji cząsteczek wykorzystamy w na naszej szkole program Molden, jeżeli ktoś zna inny program i wie, jak wyeksportować z niego do z-macierzy lub układu kartezjańskiego, to może się nim posługiwać.

Rozwiązanie równania Schrödingera prowadzi do znalezienia funkcji falowej. Funkcja ta jest wyrażona za pomocą orbitali molekularnych, które z kolei są kombinacjami liniowymi orbitali atomowych. Orbitale atomowe, w przybliżonej postaci, podaje się jako tzw. bazę atomowa. Najbardziej popularnymi bazami są bazy korzystające z funkcji Gaussa (G). Minimalną taką bazą, składającą się jedynie z orbitali obsadzonych w stanie podstawowym atomu jest baza STO-3G zawierająca konieczną liczbę funkcji dla każdego atomu. Bazę tę stosuje się dla bardzo dużych układów, lub w obliczeniach semiempirycznych. Bazy rozszerzone o dodatkowe orbitale o wyższych głównych liczbach kwantowych to na przykład 3-21G, 6-31G, 6-311G. Bazy te nazywamy bazami Gaussowskimi lub Poplowskimi. W notacji tych baz spotykamy dodatkowe oznaczenie nie wspierane już od najnowszej rewizji Gaussiana 03 (rev E) w postaci gwiazdki - *, bądź z podanymi orbitalami w nawiasie - p, d, f. Jest to uwzględnienie funkcji polaryzacyjnych na atomach drugiego i wyższych okresów np.: 6-31G(d) (inny zapis 6-31G*) baza z dodatkową funkcją dla orbitalu d dla ciężkich atomach; 6-31G(d,p) (inny zapis 6-31G**) baza z dodatkowymi funkcjami dla ciężkich atomów (orbital d) oraz dla atomów wodoru funkcje dla orbitalu p. Funkcje polaryzacyjne umożliwiają zmianę kształtu orbitali i są stosowane dla średniej wielkości molekuł. Dodatkowe funkcję bazy to funkcje rozmyte zaznaczmy je w bazie Gaussowskiej poprzez użycie znaku +. Podobnie jak wyżej użycie dwóch ++ powoduje dodanie funkcji polaryzacyjnej także na atomach wodoru. Funkcje te stosowane są dla układów, w którym mamy duże odległości między elektronem a jądrem atomowym np.: dla cząsteczek z wolną parą elektronową, anionów, układów wzbudzonych, lub z układami z wiązaniem wodorowym. Oprócz baz Gaussowskich możemy stosować inne bazy, np.: Dunningowskie: cc-PVDZ, z funkcjami polaryzacyjnymi aug-cc-PVDZ, lub specjalistyczne na przykład Huizinga czy IGLO. Więcej informacji na temat różnych baz a także same bazy można znaleźć na stronie:
http://www.emsl.pnl.gov/forms/basisform.html
Po doborze, odpowiedniego sposobu opisu funkcji, następnym etapem jest wybór przybliżenia, które pozwoli na rozwiązanie równania Schrödingera. Energie układu możemy wyznaczyć stosując różne metody i tak między innymi w metodzie HF (Hartree Fock) nie uwzględniamy korelacji między elektronami. Metody oparta na funkcji HF, lecz uwzględniające korelacje między elektronami to między innymi MP2, która jest już bardziej wymagająca obliczeniowo, lecz daje lepsze wyniki. Ale ciągle są to metody przybliżone oparte na jednym wyznaczniku Slatera. Metody oparte na rozwiązywaniu równania Schrödingera poprzez zastosowanie podstawowych praw mechaniki kwantowej nazywamy metodami ab initio.
Inne metody to metody półempiryczne polegające na założeniu, że elektrony i orbitale wewnątrz atomów nie biorą udziału w tworzeniu wiązań. Jedynie w tworzeniu wiązania biorą udział elektrony walencyjne, które są uwzględniane podczas obliczeń kwantowych. Pozostałe elektrony uwzględniane są jedynie jako pseudopotencjały będące imitacjami rzeczywistych powłok wewnętrznych. Metody półempiryczne różnią się od metod ab initio, dla których uwzględnia się wszystkie elektrony tym, że część danych stosowanych w obliczeniach pochodzi z badań eksperymentalnych i dokładnych obliczeń teoretycznych (czasami mówimy że są sparametryzowane). Metody półempiryczne są mało kosztowne obliczeniowo, dlatego znalazły zastosowanie do obliczeń bardzo dużych układów. Najbardziej popularne metody to: AM1, PM3, PM3MM, MNDO, INDO, CNDO.
Metody DFT (Density Functional Theory) to metody ab initio (choć niektórzy autorzy uważają je za metody półempiryczne) dające lepsze wyniki w porównaniu z metodami HF przy tych samych wymogach obliczeniowych komputerów. Metody te bazują na gęstości elektronowej. Uwzględniają one korelację między elektronami. Najpopularniejsze to B3LYP, LSDA, PW91, B3PW91, B1LYP, PBEPBE.
Metody mechaniki molekularnej (MM), opierają się na zastosowaniu mechanicznego modelu cząsteczki, w którym atomy traktowane są jak kule, a wiązania traktowane są jako sprężyny najczęściej spełniające prawo Hooka. Energia potencjalna obliczana jest jako suma wkładów pochodzących od oddziaływań deformacji wiązań, katów i kątów dwuściennych tworzonych przez atomy oraz oddziaływań elektrostatycznych i Van der Waalsa. Do opisu tych metod służą pola siłowe. Najczęściej stosowane pola to:
– AMBER, GROMOS - nadające się do białek i kwasów nukleinowych
– CHARMM i ECEPP - do białek
– EAS - do alkanów
– MM2 - do zastosowania ogólnego
Dla układów molekularnych, których chcemy badać dynamiczne i termodynamiczne właściwości możemy zastosować dynamikę molekularną. Jest ona oparta na równaniach ruchu Newtona dla atomów, którym nadawane są losowe prędkości zgodnie z rozkładem Maxwella. Oprócz dynamiki molekularnej jest jeszcze: Dynamika Langevina -u uwzględniającą rozpuszczalnik, dynamika Monte-Carlo polegająca na losowych zmianach np.: konformacyjnych i analizie energii.
Poniżej będziemy zamieszczać krótkie informacje na temat wybranych metod oraz baz funkcyjnych, w szczególności metod stosowanych w projektach.
Wielokonfiguracyjna Metoda Pola Samouzgodnionego – MCSCF
Metoda Pola Samouzgodnionego z Aktywna Przestrzenia – CASSCF
Metoda Sprzężonych Klasterów – CC
tematy prosze wyszukać w serwisie ręcznie

Podstawowym budulcem cząsteczek są atomy. Rozmiar atomu wynosi poniżej jednej dziesięciomiliardowej metra (10-10 metra, co odpowiada jednostce 1 Å - Angstrom). Składa się on z jądra atomowego, w którym skupiony jest ładunek dodatni i elektronów o ładunku ujemnym. Jądro atomowe w porównaniu z atomem jest bardzo małe i jest w nim skupiona praktycznie cała masa atomu. Jeśli chcielibyśmy powiększyć atom tak, aby jego średnica wynosiła 10 metrów, wówczas średnica jądra sięgałaby zaledwie 1 mm. Ze względu na tak dużą masę i małą objętość, oraz położenie jądra w centrum atomu, o oddziaływaniach między atomami decydują głównie elektrony. W matematycznym opisie atomów nie możemy używać fizyki klasycznej, ponieważ zjawiska zachodzące w skali atomowej nie mają odpowiednika w skali makroskopowej, dlatego do opisu zjawisk w skali atomowej stosuje się fizykę kwantową.
Chcąc opisać układ (atom lub cząsteczkę) musimy znać:
Geometrię - dla cząsteczki (układu co najmniej dwóch atomów), czyli wzajemne położenie atomów w przestrzeni. Możemy również podać geometrię początkową a następnie zoptymalizować strukturę, czyli znaleźć optymalne odległości i kąty między atomami charakteryzującymi stan równowagowy o najniższej energii.
Ładunek - jaki posiada badany układ, świadczy dla jonów o nadmiarze lub braku elektronu. Ładunek całkowity wyrażony w jednostkach atomowych przyjmuje zawsze wartości całkowite. Ładunek może również być wyrażony w ułamkach, gdy podzielony jest na indywidualne atomy w cząsteczce.
Multipletowość spinowa - jest to sposób obsadzenia poziomów energetycznych cząsteczki lub atomu. Obliczamy ją z równia 2S+1, gdzie S jest całkowitą liczbą kwantową spinu atomu lub cząsteczki. Multipletowość o wartości 1 nazywamy singletem, 2 - dubletem, 3 - trypletem, 4 - kwartetem, 5 - kwintetem, itd. Każdy elektron posiada spin równy ½ bądź -½. Dla układów, które posiadają wszystkie sparowane elektrony (S=0, sparowane elektrony posiadają spin o różnym znaku) multipletowość wynosi 1. Dla układów posiadających niesparowane elektrony (każdy niesparowany elektron ma wartość ½) multipletowość obliczamy z wzoru 2S+1 i tak na przykład:
– dla jonu, który powstał przez oderwanie bądź przyłączenie elektronu (mamy jeden niesparowany elektron, czyli wypadkowa liczba spinowa wynosi: S=½) multipletowość 2.
– dla jonu, który powstał przez oderwanie protonu od obojętnej cząsteczki związku organicznego multipletowość wynosi jeden (związek posiada wszystkie sparowane elektrony i ładunek minus jeden, wypadkowa liczba kwantowa spinu S wynosi 0).
– dla jonu, który powstał przez przyłączenie protonu na przykład karbokation powstały po przyłączeniu protonu do wiązania podwójnego multipletowość wynosi jeden (cząsteczka posiada wszystkie sparowane elektrony i ładunek plus jeden, wypadkowa liczba kwantowa spinu S wynosi 0).
Dla niektórych związków lub układów w stanie wzbudzonym mamy większą liczbę elektronów niesparowanych, zatem multipletowość jest większa. Takimi przykładami związków, które w stanie podstawowym mają wyższą multipletowość, są to cząsteczki O2 i FeCl3, które są w stanie trypletowym. Atomy, cząsteczki w stanie trypletowym posiadają dwa niesparowane elektrony.
Modelowanie Komputerowe
Modelowanie molekularne, zwane inaczej chemią obliczeniową, ma zastosowanie zarówno w chemii, biochemii, inżynierii materiałowej jak i w nanotechnologii. Rozwój komputerów oraz programów sprawił, że w ostatnich czasach stało się ono dostępne dla wszystkich, a obliczenia chemiczne można już przeprowadzać na komputerze osobistym. Koszt oraz czas badań teoretycznych jest niejednokrotnie o wiele mniejszy, niż wstępne badania praktyczne a uzyskane wyniki coraz bardziej zbliżają się do wyników eksperymentalnych. Korzystając z dobrodziejstw chemii teoretycznej, możemy już dziś z bardzo dobrymi rezultatami przewidzieć właściwości fizyczne i chemiczne, modelować reakcje oraz stany przejściowe, symulować widma spektroskopowe, czy też badać układy bardziej skomplikowane, jakim są centra aktywne enzymów. Możemy także projektować leki oraz nowe materiały. Modelowanie komputerowe często nie może dać jednoznacznej odpowiedzi na zadawane pytania, ale w znaczny sposób pomaga zrozumieć oraz rozwiązać problemy. Wszechstronnie wykształcony chemik powinien umieć korzystać z najnowszych dobrodziejstw, jakim niewątpliwie jest wsparcie badań eksperymentalnych obliczeniami.
Są różne za i przeciw modelowaniu molekularnym. Podsumowując to wszystko, warto policzyć coś samemu, żeby stwierdzić czy rzeczywiście uzyskane wyniki są warte nauki modelowania. Z drugiej strony jeżeli sami będziemy umieli policzyć pewne rzeczy zawsze możemy ubogacić naszą pracę - i tego będę chciał dla was.
Zapraszam do pisania w komentarzach argumentów za i przeciw modelowaniu.

Witam wszystkich w drugiej części wykładu poświęconych szkole. W tej części miało być o:
. - Zastosowanie wyników, prezentacja wyników, patenty
. - Wstęp modelowania
. - Co to jest modelowanie i do czego może być wykorzystane
. - Biochemia, biotechnologia
. - Nanotechnologia
. - Badanie spektroskopowe
. - Metody teoretyczne, bazy
. - - - Wielokonfiguracyjna Metoda Pola Samouzgodnionego - MCSCF
. - - - Metoda Pola Samouzgodnionego z Aktywna Przestrzenia - CASSCF
. - - - Metoda Sprzężonych Klasterów - CC,
Ze względu na fakt, że większość z nas jest doktorantami i potrafi samodzielnie szukać informacji, zrobimy mały skok - bardzo krótkie streszczenie wszystkich tematów, pominiemy te, które jeszcze nie zostały opracowane i przejdziemy do meritum szkoły, czyli praktycznego podejścia do modelowania.
Od razu zadaje zadanie na ten tydzień, proszę nauczyć się budować cząsteczki za pomocą programu Molden (lub innego dowolnego programu).
Jeśli zostanie to opanowane, to będziemy mogli podjąć się projektów i w międzyczasie uzupełniać naszą wiedzę. W następnym tygodniu przewiduję optymalizację, skan po energii potencjalnej, oraz energie oddziaływania. Tak więc zaczynamy.